1-10 11-20 21-30 31-40 41-50 51-60 61-70 71-80 81-90 91-100 101-107

LEARNING TO THINK MATHEMATICALLY: PROBLEM SOLVING,
METACOGNITION, AND SENSE-MAKING IN MATHEMATICS

Alan H. Schoenfeld
University of California at Berkeley


[Chapter 15, pp. 334-370, of the Handbook for Research on Mathematics
Teaching and Learning (D. Grouws, Ed.). New York: MacMillan, 1992.]


THE SCOPE OF THIS CHAPTER

The goals of this chapter are (a) to outline and substantiate a broad conceptualization of what it means to think mathematically,  (b) to summarize the literature relevant to understanding mathematical thinking and problem solving, and (c) to point to new directions in research, development and assessment consonant with an emerging understanding of mathematical thinking and the goals for instruction outlined here.

The choice of the phrase "learning to think mathematically" in this chapter's title is deliberately broad. Although the original charter for this chapter was to review the literature on problem solving and metacognition, those two literatures themselves are somewhat ill-defined and poorly grounded. As the literature summary will make clear, problem solving has been used with multiple meanings that range from "working rote exercises" to "doing mathematics as a professional;" metacognition has multiple and almost disjoint meanings (e.g. knowledge about one's thought processes, self-regulation during problem solving) which make it difficult to use as a concept. The chapter outlines the various meanings that have been ascribed to these terms, and discusses their role in mathematical thinking. The discussion will not have the character of a classic literature review, which is typically encyclopedic in its references and telegraphic in its discussions of individual papers or results. It will, instead, be selective and illustrative, with main points illustrated by extended discussions of pertinent examples.

Problem solving has, as predicted in the 1980 Yearbook of the National Council of Teachers of Mathematics (Krulik, 1980, p. xiv), been the theme of the 1980's. The decade began with NCTM's widely heralded statement, in its Agenda for Action, that "problem solving must be the focus of school mathematics" (NCTM, 1980, p.1). It concluded with the publication of Everybody Counts  (National Research Council, 1989) and the Curriculum and Evaluation Standards for School Mathematics (NCTM,1989), both of which emphasize problem solving. One might infer, then,that there is general acceptance of the idea that the primary goal of mathematics instruction should be to have students become competent problem solvers. Yet, given the multiple interpretations of the term, the goal is hardly clear. Equally unclear is the role that problem solving, once adequately characterized, should play in the larger context of school mathematics. What are the goals for mathematics instruction, and how does problem solving fit within those goals?

Such questions are complex. Goals for mathematics instruction depend on one's conceptualization of what mathematics is, and what it means to understand mathematics. Such conceptualizations vary widely. At one end of the spectrum, mathematical knowledge is seen as a body of facts and procedures dealing with quantities, magnitudes, and forms, and relationships among them; knowing mathematics is seen as having "mastered" these facts and procedures. At the other end of the spectrum, mathematics is conceptualized as the "science of patterns," an (almost) empirical discipline closely akin to the sciences in its emphasis on pattern- seeking on the basis of empirical evidence.

The author's view is that the former perspective trivializes mathematics, that a curriculum based on mastering a corpus of mathematical facts and procedures is severely impoverished -- in much the same way that an English curriculum would be considered impoverished if it focused largely, if not exclusively, on issues of grammar. He has, elsewhere, characterized the mathematical enterprise as follows.

Mathematics is an inherently social activity, in which a community of trained practitioners (mathematical scientists) engages in the science of patterns -- systematic attempts, based on observation, study, and experimentation, to determine the nature or principles of regularities in systems defined axiomatically or theoretically ("pure mathematics") or models of systems abstracted from real world objects ("applied mathematics"). The tools of mathematics are abstraction, symbolic representation, and symbolic manipulation. However, being trained in the use of these tools no more means that one thinks mathematically than knowing how to use shop tools makes one a craftsman. Learning to think mathematically means (a) developing a mathematical point of view -- valuing the processes of mathematization and abstraction and having the predilection to apply them, and (b) developing competence with the tools of the trade, and using those tools in the service of the goal of understanding structure -- mathematical sense-making. (Schoenfeld, forthcoming)

This notion of mathematics has gained increasing currency as the mathematical community has grappled, in recent years, with issues of what it means to know mathematics and to be mathematically prepared for an increasingly technological world. The following quotation from Everybody Counts  typifies the view, echoing themes in the NCTM Standards (NCTM, 1989) and Reshaping School Mathematics  (National Research Council, 1990a).

Mathematics is a living subject which seeks to understand patterns that permeate both the world around us and the mind within us. Although the language of mathematics is based on rules that must be learned, it is important for motivation that students move beyond rules to be able to express things in the language of mathematics. This transformation suggests changes both in curricular content and instructional style. It involves renewed effort to focus on:

As teaching begins to reflect these emphases, students will have opportunities to study mathematics as an exploratory, dynamic, evolving discipline rather than as a rigid, absolute, closed body of laws to be memorized. They will be encouraged to see mathematics as a science, not as a canon, and to recognize that mathematics is really about patterns and not merely about numbers. (National Research Council, 1989, p. 84)

From this perspective, learning mathematics is empowering. Mathematically powerful students are quantitatively literate. They are capable of interpreting the vast amounts of quantitative data they encounter on a daily basis, and of making balanced judgments on the basis of those interpretations. They use mathematics in practical ways, from simple applications such as using proportional reasoning for recipes or scale models, to complex budget projections, statistical analyses, and computer modeling. They are flexible thinkers with a broad repertoire of techniques and perspectives for dealing with novel problems and situations. They are analytical, both in thinking issues through themselves and in examining the arguments put forth by others.

This chapter is divided into three main parts, the first two of which constitute the bulk of the review. Part I, "Toward an understanding of mathematical thinking," is largely historical and theoretical, having as its goals the clarification of terms like problem, problem solving,  and doing mathematics . It begins with "Immediate Background: Curricular trends in the latter 20th Century," a brief recapitulation of the curricular trends and social imperatives that produced the 1980's focus on problem solving as the major goal of mathematics instruction. The next section,"On problems and problem solving: Conflicting definitions," explores contrasting ways in which the terms problem and problem solving have been used in the literature, and the contradictions that have resulted from the multiple definitions and the epistemological stances underlying them. "Enculturation and cognition" outlines recent findings suggesting the large role of cultural factors in the development of individual understanding. "Epistemology, ontology, and pedagogy intertwined" describes current explorations into the nature of mathematical thinking and knowing, and the implications of these explorations for mathematical instruction. Part I concludes with "Goals for instruction, and a pedagogical imperative."

Part II, "A framework for understanding mathematical cognition," provides more of a classical empirical literature review. "The framework" briefly describes an overarching structure for the examination of mathematical thinking that has evolved over the past decade. It will be argued that all of these categories -- core knowledge, problem solving strategies, effective use of one's resources, having a mathematical perspective, and engagement in mathematical practices -- are fundamental aspects of thinking mathematically. The sections that follow elaborate on empirical research within the categories of the framework. "Resources" describes our current understanding of cognitive structures: the constructive nature of cognition, cognitive architecture, memory, and access to it. "Heuristics" describes the literature on mathematical problem solving strategies. "Monitoring and control" describes research related to the aspect of metacognition known as self- regulation. "Beliefs and affects" considers individuals' relationships to the mathematical situations they find themselves in, and the effects of individual perspectives on mathematical behavior and performance. Finally, "Practices" focuses on the practical side of the issue of socialization discussed in Part I, describing instructional attempts to foster mathematical thinking by creating microcosms of mathematical practice.

Part III, "Issues," raises some practical and theoretical points of concern as it looks to the future. It begins with a discussion of issues and terms that need clarification, and of the need for an understanding of methodological tools for inquiry into problem solving. It continues with a discussion of unresolved issues in each of the categories of the framework discussed in Part II, and concludes with a brief commentary on important issues in program design, implementation, and assessment. The specification of new goals for mathematics instruction consonant with current understandings of what it means to think mathematically carries with it an obligation to specify assessment techniques -- means of determining whether students are achieving those goals. Some preliminary steps in those directions are considered.

PART I

TOWARD AN UNDERSTANDING OF "MATHEMATICAL THINKING"

Immediate Background: Curricular trends in the latter 20th Century

The American mathematics education enterprise is now undergoing extensivescrutiny, with an eye toward reform. The reasons for the re-examination, and for a major overhaul of the current mathematics instruction system, are many and deep. Among them are the following.

The 1980's, of course, are not the first time that the American mathematics enterprise has been declared "in crisis."A major renewal of mathematics and science curricula in the United States was precipitated on October 4, 1957 by the Soviet Union's successful launch of the space satellite Sputnik. In response to fears of impending Soviet technological and military supremacy, scientists and mathematicians became heavily involved in the creation of new educational materials, often referred to collectively as the alphabet curricula (e.g. SMSG in mathematics, BSCS in biology, PSSC in physics). In mathematics, the new math  flourished briefly in the 1960's, and then came to be perceived of as a failure. The general perception was that students had not only failed to master the abstract ideas they were being asked to grapple with in the new math, but that in addition they had failed to master the basic skills that the generations of students who preceded them in the schools had managed to learn successfully. In a dramatic pendulum swing, the new math was replaced by the back to basics movement. The idea, simply put, was that the fancy theoretical notions underlying the new math had not worked, and that we as a nation should make sure that our students had mastered the basics -- the foundation upon which higher order thinking skills were to rest.

By the tail end of the 1970's it became clear that the back to basics movement was a failure. A decade of curricula that focused on rote mechanical skills produced a generation of students who, for lack of exposure and experience, performed dismally on measures of thinking and problem solving. Even more disturbing, they were no better at the basics than the students who had studied the alphabet curricula. The pendulum began to swing in the opposite direction, toward "problem solving."The first major call in that direction was issued by the National Council of Supervisors of Mathematics in 1977. It was followed by the National Council of Teachers of Mathematics' (1980) Agenda for Action , which had as its first recommendation that "problem solving be the focus of school mathematics."Just as back to basics was declared to be the theme of the 1970's, problem solving was declared to be the theme of the 1980's (See, e.g., Krulik, 1980). Here is one simple measure of the turn-around. In the 1978 draft program for the 1980 International Congress on Mathematics Education (ICME IV, Berkeley, California, 1980: see Zweng, Green, Kilpatrick, Pollak, & Suydam, 1983), only one session on problem solving was planned, and it was listed under "unusual aspects of the curriculum." Four years later, problem solving was one of the seven main themes of the next International Congress (ICME V, Adelaide, Australia: See Burkhardt, Groves, Schoenfeld, & Stacey, 1988; Carss, 1986). Similarly, "metacognition" was coined in the late 1970's, appeared occasionally in the mathematics education literature of the early 1980's, and then with ever-increasing frequency through the decade. Problem solving and metacognition, the lead terms in this article's title, are perhaps the two most overworked -- and least understood -- buzz words of the 1980's.

This chapter suggests that, on the one hand, much of what passed under the name of problem solving during the 1980's has been superficial, and that were it not for the current "crisis," a reverse pendulum swing might well be on its way. On the other hand, it documents that we now know much more about mathematical thinking, learning, and problem solving than during the immediate post-Sputnik years, and that a reconceptualization both of problem solving and of mathematics curricula that do justice to it is now possible. Such a reconceptualization will in large part be based in part on advances made in the past decade: detailed understandings of the nature of thinking and learning, of problem solving strategies and metacognition; evolving conceptions of mathematics as the "science of patterns" and of doing mathematics as an act of sense-making; and of cognitive apprenticeship and "cultures of learning."

On problems and problem solving: Conflicting definitions

In a historical review focusing on the role of problem solving in the mathematics curriculum, Stanic and Kilpatrick (1989, page 1) provide the following brief summary:

Problems have occupied a central place in the school mathematics curriculum since antiquity, but problem solving has not. Only recently have mathematics educators accepted the idea that the development of problem solving ability deserves special attention. With this focus on problem solving has come confusion. The term problem solving has become a slogan encompassing different views of what education is, of what schooling is, of what mathematics is, and of why we should teach mathematics in general and problem solving in particular.

Indeed, "problems" and "problem solving" have had multiple and often contradictory meanings through the years -- a fact that makes interpretation of the literature difficult. For example, a 1983 survey of college mathematics departments (Schoenfeld, 1983) revealed the following categories of goals for courses that were identified by respondents as "problem solving" courses:

The two poles of meaning indicated in the survey are nicely illustrated in two of Webster's 1979, p. 1434) definitions for the term "problem:"


Definition 1: "In mathematics, anything required to be done, or requiring the doing of something."

Definition 2: "A question... that is perplexing or difficult."

Problems as routine exercises

Webster's Definition 1, cited immediately above, captures the sense of the term problem as it has traditionally been used in mathematics instruction. For nearly as long as we have written records of mathematics, sets of mathematics tasks  have been with us -- as vehicles of instruction, as means of practice, and as yardsticks for the acquisition of mathematical skills. Often such collections of tasks are anything but problemsin the sense of the second definition. They are, rather, routine exercises organized to provide practice on a particular mathematical technique that, typically, has just been demonstrated to the student. We begin this section with a detailed examination of such problems, focusing on their nature, the assumptions underlying their structure and presentation, and the consequences of instruction based largely, if not exclusively, in such problem sets. That discussion sets the context for a possible alternative view.

A generic example of a mathematics problem set, with antecedents that Stanic and Kilpatrick trace to antiquity, is the following excerpt from a late 19th century text, W. J. Milne's (1897) A Mental Arithmetic. The reader may wish to obtain an answer to problem 52 by virtue of mental arithmetic before reading the solution Milne provides.

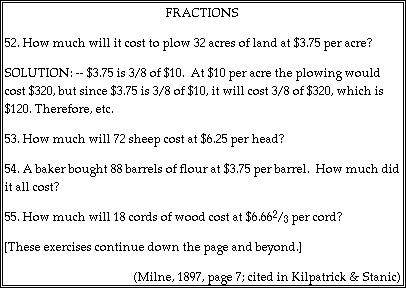
IMAGE Imgs/Learning_to_think_Math01.gif

The particular technique students are intended to learn from this body of text is illustrated in the solution of problem 52. In all of the exercises, the student is asked to find the product (A x B), where A is given as a two-digit decimal that